
셀프 넘버 성공출처다국어분류
|
시간 제한 |
메모리 제한 |
제출 |
정답 |
맞은 사람 |
정답 비율 |
|
1 초 |
256 MB |
56038 |
28453 |
22966 |
50.972% |
https://www.acmicpc.net/problem/4673
4673번: 셀프 넘버
셀프 넘버는 1949년 인도 수학자 D.R. Kaprekar가 이름 붙였다. 양의 정수 n에 대해서 d(n)을 n과 n의 각 자리수를 더하는 함수라고 정의하자. 예를 들어, d(75) = 75+7+5 = 87이다. 양의 정수 n이 주어졌을 때,
www.acmicpc.net
문제
셀프 넘버는 1949년 인도 수학자 D.R. Kaprekar가 이름 붙였다. 양의 정수 n에 대해서 d(n)을 n과 n의 각 자리수를 더하는 함수라고 정의하자. 예를 들어, d(75) = 75+7+5 = 87이다.
양의 정수 n이 주어졌을 때, 이 수를 시작해서 n, d(n), d(d(n)), d(d(d(n))), ...과 같은 무한 수열을 만들 수 있다.
예를 들어, 33으로 시작한다면 다음 수는 33 + 3 + 3 = 39이고, 그 다음 수는 39 + 3 + 9 = 51, 다음 수는 51 + 5 + 1 = 57이다. 이런식으로 다음과 같은 수열을 만들 수 있다.
33, 39, 51, 57, 69, 84, 96, 111, 114, 120, 123, 129, 141, ...
n을 d(n)의 생성자라고 한다. 위의 수열에서 33은 39의 생성자이고, 39는 51의 생성자, 51은 57의 생성자이다. 생성자가 한 개보다 많은 경우도 있다. 예를 들어, 101은 생성자가 2개(91과 100) 있다.
생성자가 없는 숫자를 셀프 넘버라고 한다. 100보다 작은 셀프 넘버는 총 13개가 있다. 1, 3, 5, 7, 9, 20, 31, 42, 53, 64, 75, 86, 97
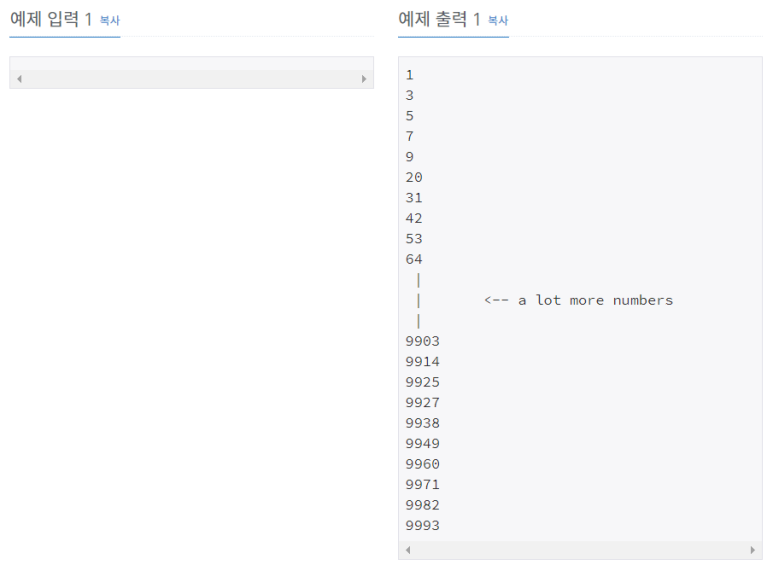
10000보다 작거나 같은 셀프 넘버를 한 줄에 하나씩 출력하는 프로그램을 작성하시오.
입력
입력은 없다.
출력
10,000보다 작거나 같은 셀프 넘버를 한 줄에 하나씩 증가하는 순서로 출력한다.
알고리즘 분류
백준 알고리즘 # 4673번 : 셀프 넘버

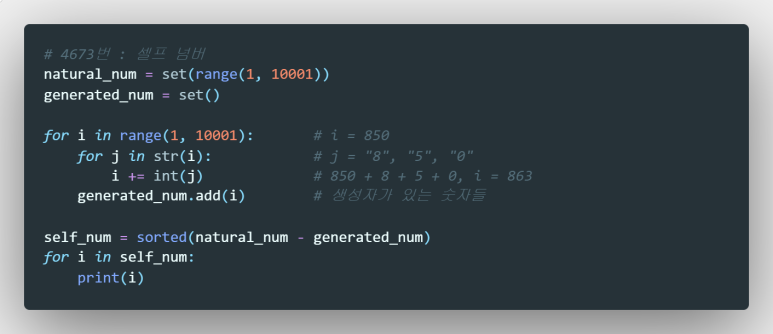
natural_num = set(range(1, 10001))
generated_num = set()
for i in range(1, 10001): # i = 850
for j in str(i): # j = "8", "5", "0"
i += int(j) # 850 + 8 + 5 + 0, i = 863
generated_num.add(i) # 생성자가 있는 숫자들
self_num = sorted(natural_num - generated_num)
for i in self_num:
print(i)풀이
처음에 문제에 대한 이해가 힘들어서, 아래 블로그의 포스팅을 참고하면서 문제를 이해했어요.
(설명 완전 잘 되있어요👍👍)
[백준/4673/파이썬3(python3)] 셀프 넘버
문제 셀프 넘버는 1949년 인도 수학자 D.R. Kaprekar가 이름 붙였다. 양의 정수 n에 대해서 d(n)을 n과 n의 각 자리수를 더하는 함수라고 정의하자. 예를 들어, d(75) = 75+7+5 = 87이다. 양의 정수 n이 주어졌�
this-programmer.com
앞에서 부터 자연수를 set 함수를 사용해서 1부터 10000까지 natural_num로 변수설정을 하고
생성될 숫자를 generated_num이라는 변수로 만들어둔다.
그 다음 1부터 10000까지 for 반복문을 돌리고 이 반복문 안에 2중 반복문으로
입력되는 i를 str(문자열)로 바꿔줘서
예를 들어 850이라는 i가 입력될 때 8, 5, 0 처럼 하나하나씩 떼어서 더해줄 수 있도록하고
그 안에서 850 + 8 + 5 + 0을 해준 결과인 863을 generated_num 변수에 넣어준다.
이렇게 하면 결국 generated_num 변수에는 생성자로 생겨난 수들이 모이게 되고
셀프 넘버는 생성자가 없는 숫자(1, 3, 5, 7, 9 등)이니
전체 자연수(natural_num)에서 생성자가 모인 변수(generated_num)을 빼주면 셀프 넘버만 남게 된다.
마지막으로 이것을 for문을 이용해서 한 줄씩 출력해주면 끄--읏!👊
자세한 코드가 궁금하신 분들은 아래 GitHub 참고해주세요🙏
wook2124/Algorithm
Practice algorithm. Contribute to wook2124/Algorithm development by creating an account on GitHub.
github.com
최종 소스코드
'코딩테스트 > 백준 알고리즘' 카테고리의 다른 글
| 백준 알고리즘 | 10809 : 알파벳 찾기 (Python / 파이썬) (0) | 2020.09.21 |
|---|---|
| 백준 알고리즘 | 1065 : 한수 (Python / 파이썬) (0) | 2020.09.19 |
| 백준 알고리즘 | 8958 : OX퀴즈 (Python / 파이썬) (0) | 2020.09.19 |
| 백준 알고리즘 | 3052 : 나머지 (Python / 파이썬) (0) | 2020.09.19 |
| 백준 알고리즘 | 2562 : 최댓값 (Python / 파이썬) (0) | 2020.09.18 |




댓글